Consider the Two Dimensional Agains the Flat Plate
Abstract
This paper concerns the flow of fluid exiting a 2-dimensional pipe and impacting an infinite wedge. Where the menstruation leaves the pipe there is a complimentary surface between the fluid and a passive gas. The model is a generalisation of both airplane bubbles and flow impacting a flat plate. In the absence of gravity and surface tension, an exact free streamline solution is derived. Nosotros also construct two numerical schemes to compute solutions with the inclusion of surface tension and gravity. The first method involves mapping the flow to the lower half-aeroplane, where an integral equation apropos only boundary values is derived. This integral equation is solved numerically. The 2nd method involves conformally mapping the flow domain onto a unit disc in the s-plane. The unknowns are then expressed as a power series in s. The series is truncated, and the coefficients are solved numerically. The boundary integral method has the additional advantage that it allows for solutions with waves in the far-field, as discussed later. Good understanding between the two numerical methods and the exact free streamline solution provides a cheque on the numerical schemes.
Introduction
In this newspaper, we consider a classical two-dimensional potential free surface flow. Fluid comes in via a pipe, which is placed higher up a wedge with internal angle \(\beta \). The incoming flow travels in the direction of gravity. The menstruum is forcibly separated from the piping, and a complimentary surface is formed. The menses configuration is shown in Fig. i. This model is a generalisation of plane bubbles (when \(\beta =\pi \)), the subject of a diversity of previous studies [one,2,iii,4,v,6,7,8]. While some of these works are more analytic in their approach (for instance, see [2, three]), the majority of previous investigations make employ of a numerical method referred to in literature as series truncation methods. The flow domain is mapped to a unit disc, and the complex velocity \(\xi \) is expressed in terms of a power serial in the mapped infinite. To ensure that the serial is convergent, all leading order singularities must exist accounted for in the series representation of \(\xi \). The space series is truncated, and the coefficients are found by satisfying the relevant boundary conditions at a discrete set of points on the boundaries. The method is an case of an changed problem, where the boundary is found after having solved the system of equations. In a series of papers, Vanden-Broeck [6,7,8] used this method (originally considered with less meshpoints by Birkhoff and Carter [1]) to notice plane bubbles both excluding and including surface tension. Previous authors have also investigated this model using a boundary integral method using a Green'south function arroyo both with [9] and without [10] surface tension. The nature of the solution spaces in both cases is discussed in Sect. vi.
The model in this paper is also a generalisation (when \(\beta =\pi /ii\)) of flow exiting a pipe and impacting a plate. This model was considered with the furnishings of gravity included by Christodoulides and Dias [xi], who too made employ of a series truncation method. In this newspaper, nosotros meliorate the convergence of their series past including the Stokes far-field singularity associated with free surfaces experiencing gravity that approach a uniform stream. We also compute solutions including the effects of surface tension, where waves are seen in the far-field. To allow for the inclusion of waves, nosotros use a boundary integral method, based upon using Cauchy's integral formula to limited unknowns in terms of purlieus values, as opposed to the series truncation method described in a higher place. This method has been used by a multifariousness of authors for a range of models: flows past obstructions [12, thirteen], flows under sluice gates [14,15,sixteen], and costless surface gravity–capillary waves [17,18,nineteen] to proper name simply a few. We notation that boundary integral equation methods based on Green's functions tin can also exist used. It is shown in [20] that both types of methods yield comparable results. Here we chose to utilize purlieus integral equation methods based on Cauchy'southward integral formula and then that all the schemes in the paper use \(\phi \) and \(\psi \) as independent variables.
Equally well equally the two particular cases described higher up, we besides solve for the more general instance when \(\beta \in (\pi /2,\pi )\). This models the menstruum exiting a piping and impacting a wedge. We find that the solution space is similar to that of plane bubbles. This is expected, due to the similar singularity construction of \(\eleven \) in the flow domain, every bit shown in Sect. v. In item, when gravity is included, both plane bubbles and flows impacting a wedge approach an minute jet downstream. On the other mitt, flows that impact a flat plate (which is perpendicular to gravity) approach either a compatible stream or a periodic wave train. When budgeted a uniform stream, both the boundary integral method and the series truncation method are viable. If the menses approaches a periodic wave train, nosotros must apply the boundary integral method, since \(\xi \) is no longer divers at infinity downstream. We also derive an exact free streamline solution (where both gravity and surface tension are negligible) using the methodology establish in [21, 22]. Practiced agreement between the analytic free streamline solution and both numerical methods provides a check on our numerical schemes. We note that this model with simply capillary effects was explored recently in [23].
A cardinal characteristic of the model is the angle at which the gratis surface separates from the pipe, denoted \(\mu \). For free streamline flow, this value must exist \(\mu =\pi \), known every bit shine separation. Curiously, this local behaviour is known to have a singularity in the curvature at the separation point [24]. For pure gravity flows, there are just three permissible angles [25]: \(\pi /two\), \(2\pi /3\), and \(\pi \). For pure capillary flows, the situation is more complicated. The first in-depth analytic investigations were made by [26] and [27], who plant local behaviours near the separation point with weak capillarity. Their analysis assumes that the separation remains smooth as in the complimentary streamline case (that is, \(\mu =\pi \)). The motivation for this appears physical: the free streamline solution has a singularity in the curvature at the separation signal, so including the curvature explicitly in the boundary condition could regulate this. They discover an inner solution by linearising the system virtually the separation bespeak. The linearised organisation does not have a unique solution. In [26], a solution which is not singular at the separation point is chosen. It is plant the solution has spurious waves on the interface. In [27], they choose a solution with no waves, but is singular. They try to rectify this singularity (which invalidated the asymptotic analysis) past finding an inner–inner solution, but where unable to satisfy matching atmospheric condition. The problem was considered again by [28], who this time allows the separation bending to not be \(\mu =\pi \). Surprisingly, this makes the solution more singular than the free streamline solution, for which the singularity only occurs in the curvature. They successfully match this inner solution with the outer gratis streamline. This behaviour was then found for a variety of capillary flows with separations: both asymptotically for weak capillarity (for case [29]) and the exploration numerically of these solution branches into regimes where surface tension is of the same order as inertia (for a review, meet [thirty]). For gravity–capillary solutions, information technology is establish that whatever value of \(\mu \) is permissible (meet Chap. 3 of [30]). This is incorporated into the numerical method by taking \(\mu \) as an unknown which must be found every bit part of the solution.
To summarise, in this paper, we compute solutions to the flow geometry shown in Fig. 1 with \(\beta \in [\pi /2,\pi ]\) for three cases: when there is no gravity or surface tension, when there is gravity but no surface tension, and with the inclusion of both gravity and surface tension. An exact free streamline solution is found. Solutions with gravity and surface tension are institute using either a serial truncation method or a boundary integral method.
The paper is organised every bit follows. Section 2 is the formulation. Section 3 is the derivation of the exact free streamline solution. Section four is a description of the purlieus integral method. Section five is a clarification of the series truncation method. Section 6 contains the results of the paper. Section 7 is a conclusion.

Menses configuration in the z-plane. The altitude in the 10 direction from the pipe to the origin is divers every bit WH and so that the corresponding dimensionless quantity is W
Formulation
Consider the problem of flow exiting a pipe and impacting a wedge. Nosotros choose Cartesian coordinates, with 10 pointing in the direction of gravity, and the origin placed at the tip of the wedge. Flow comes in via a ii-dimensional pipe of width iiH at \(x\rightarrow -\infty \), where the fluid travels with constant velocity U in the positive x direction. We take H every bit the reference length and U every bit the reference velocity. The flow separates where the pipe ends with separation angle \(\mu \). Below the pipage is a wedge, placed such that the tip lies beneath the center of the pipe. At that place exists a central streamline which meets the wedge at a stagnation point. The angle between the central streamline and the wedge is given by \(\beta \), and the wedge is at a nondimensional distance West in the x direction below the end of the pipe. We assume the menses is steady, and the catamenia configuration is shown in Fig. 1.
We denote the velocity vector as \(\mathbf {u}=(u,v)\), where u and v are the components of the velocity in the x and y directions. Nosotros will assume that the fluid is incompressible and the flow is irrotational, and hence we can write the velocity field in terms of 2 harmonic functions, the velocity potential \(\phi \) and the streamfunction \(\psi \), divers such that
$$\begin{aligned} u = \phi _x = \psi _y, \quad v = \phi _y = -\psi _x. \terminate{aligned}$$
(1)
Without loss of generality, nosotros choose \(\phi =0\) at the separation point, and \(\psi =0\) on the central streamline. Nosotros denote the value of \(\phi \) at the tip of the wedge as \(\phi _B\). In this scaling, the streamline along the wall at \(y=i\) and complimentary surface are given past \(\psi =i\). We also define the complex potential \(f=\phi +\mathrm{{i}}\psi \). When solving this problem, we will conformally map the flow domain to some auxiliary space with preferable geometry. Via the theory of analytic functions, the governing equation can be handled by enervating the function \(\xi =u-\mathrm{{i}}v\) is an analytic function of \(z=x+\mathrm{{i}}y\). The problem and then reduces to finding an analytic function such that the relevant boundary weather condition are satisfied.
Since the complimentary surface is unknown a priori, as well as the kinematic boundary status, we require a dynamic boundary condition. The nondimensionalised Bernoulli equation on the free surface (denoted \(x=\eta (y)\)) is given by
$$\begin{aligned} q^2 - \frac{ii}{F^2} x + \frac{2}{\alpha } \kappa = B \quad \text {for} \,\, 10=\eta (y). \stop{aligned}$$
(two)
Here \(q=|\mathbf {u} |\), \(\kappa \) is the mean curvature (counted positive when the centre of curvature lies inside the fluid), and F and \(\alpha \) are the Froude number and Weber number, respectively, given by
$$\brainstorm{aligned} F = \frac{U}{\sqrt{gH}}, \quad \alpha = \frac{\rho U^2 H}{T}. \finish{aligned}$$
(three)

3 flow configurations: a menses from a pipe with no obstruction (plane bubble), b menses onto wedge c period onto plate
Due to the symmetry of the problem about the line \(y = 0\), we tin restrict our attention to the problem in \(0 \le \psi \le 1\) (\(y\ge 0\)). Recalling that x points in the direction of gravity, the purlieus weather condition in the z-aeroplane are
$$\brainstorm{aligned}&5 = 0 \quad \text {for} \,\, ten<0, \, y=0 , \end{aligned}$$
(4)
$$\begin{aligned}&five = 0 \quad \text {for} \,\, x\in (-\infty ,-Due west], \, y=i, \end{aligned}$$
(5)
$$\brainstorm{aligned}&v = u\tan \beta \quad \text {for} \,\, ten>0, \,\,\, y=-x\tan \beta , \,\, \end{aligned}$$
(6)
$$\begin{aligned}&q^ii - \frac{2}{F^ii} \eta (y) + \frac{2}{\alpha } \kappa = B \quad \text {for} \,\, ten=\eta (y) . \end{aligned}$$
(7)
For the case of \(\beta =\pi \), this problem becomes that of period exiting a piping. An example of a solution is shown in Fig. 2a. The key streamline \(\psi =0\) no longer hits a wedge, but becomes a line of symmetry. Since we are dealing with inviscid potential catamenia, we can take this line of symmetry to be a wall. Furthermore, we tin can utilize the symmetry near the streamline \(\psi =-i\). Viewed this way, nosotros meet that this problem is so equivalent to that of a plane chimera. The separation bending \(\mu \) is now the angle between the primal streamline and the chimera surface. This trouble was solved numerically for finite F both when \(\alpha ^{-1} =0\) (i.due east. no surface tension) and with finite \(\alpha \) in a sequence of papers [6,7,8]. The costless streamline solution (\(F\rightarrow \infty \) and \(\alpha \rightarrow \infty \)) solution is just a uniform stream.
When \(\beta =\pi /2\), this problem becomes that of flow exiting a pipe onto a flat plate. This was solved numerically when \(\alpha ^{-1}=0\) by Christodoulides and Dias [11]. We volition provide a modification to their numerical scheme to solve the more general problem with arbitrary \(\beta \). Figure 2(b) shows a typical solution. We also present a new numerical scheme based upon representing the unknowns via an integral equation concerning solely values on the boundary. The necessity for this new method is that information technology allows for waves in the far-field, a feature solutions with finite surface tension showroom for this model. One such solution is shown in Fig. 2c. Even so, first, we will present an exact solution to this problem, nether the assumption that both gravity and surface tension are negligible (\(F\rightarrow \infty , \alpha \rightarrow \infty \)).
Gratis streamline solution
We volition present an exact solution for the flow configuration shown in Fig. 1 nether the assumption that gravity and surface tension are both negligible, using a method devised by Love [21]. The method was modified by Hopkinson [22] to permit for internal singularities, and revisited recently by Eggers and Smith [31]. This problem was solved by [24] under the assumption that the wedge was of finite length (run into Chap. 2.7). Bernoulli's equation (ii) now gives that
$$\begin{aligned} q = \text {abiding} . \end{aligned}$$
(8)
We restrict our attending to \(0\le \psi \le 1\), noting that the solution for \(-one\le \psi <0\) is constitute by reflecting the menses across the streamline ABD. Throughout this paper, points A, B, C, and D will refer to the points as shown in Fig. 3 (A is the flow upstream, B where the two walls meet, C the separation indicate, and D is downstream). Nosotros annotation that the configuration shown in Fig. 3 is the same as that shown in Fig. i, but with \(\mu =\pi \). No other value of \(\mu \) is possible, since if \(\mu <\pi \), then the value of q at the separation betoken C is zero, while if \(\mu >\pi \), then it is infinite. This tin can exist shown by noting that the local behaviour at the separation point is a menstruum inside a corner with interior angle \(\mu \), which is given by
$$\brainstorm{aligned} f\sim z^{\pi /\mu }, \,\,\,\,\,\,\, \,\,\,\,\,\,\,\,\,\,\,\,\,\, \eleven \sim z^{\pi /\mu -1}, \end{aligned}$$
(9)
where f and \(\eleven \) are the complex potential and circuitous velocity, respectively. From this, ane can see that as \(z\rightarrow 0\), \(|\eleven |\rightarrow \infty \) if \(\mu >\pi \), while if \(\mu <\pi \), \(\xi \rightarrow 0\). In either case, Eq. (8) cannot exist satisfied. We note hither that the inclusion of gravity and capillarity allows for different values of \(\mu \). Observing that there exist infinite velocities at the separation indicate when \(\mu >\pi \), it must exist that \(\mu \le \pi \) when surface tension is ignored, or else (vii) cannot exist satisfied. In fact, it is known that when ignoring surface tension, but three values of \(\mu \) can satisfy Eq. (7): \(\mu =\pi /2,\) \(2\pi /3\), and \(\pi \) [25]. The event of capillarity on the separation angle has been the subject area of intense written report ([26,27,28,29, 32,33,34], and for a review, [30]). It has been found that when surface tension is included, any value of \(\mu \) is permissible (that is, local assay does non restrict the possible values of \(\mu \) to a discrete fix). This is considering the infinite velocity occurring when \(\mu >\pi \) tin can be counterbalanced with infinite values of the curvature. Hence, when numerically calculating gravity–capillary flows, the value \(\mu \) must be included as an unknown.

Flow configuration in the z-plane. Dashed curves are streamlines
We solve the free streamline trouble by conformally mapping the trouble on to an auxilliary t-plane, which we take to be the lower half-plane, such that all boundaries map onto the existent axis. The t-aeroplane is shown in Fig. 4. This mapping is found by guessing a complex potential f(t) which will requite u.s.a. the desired properties of the period. Full details can exist establish in [22], but for this problem, we take f(t) to exist a point sink at the origin, given past
$$\begin{aligned} f(t) = -\frac{1}{\pi } \log t. \end{aligned}$$
(x)
The streamline ABD is mapped onto the positive existent axis, while the streamline ACD is mapped onto the negative real axis in the t-airplane. The point C maps to \(t=-one\), and B maps to \(t=d\), where
$$\begin{aligned} d = \mathrm{due east}^{-\pi \phi _B}. \end{aligned}$$
(11)
Denoting \(\xi = \mathrm{e}^{\tau -\mathrm{{i}}\theta }\), we ascertain \(\varOmega \) to be the function
$$\begin{aligned} \varOmega = \log \frac{\mathrm{d}z}{\mathrm{df}} = \log \frac{1}{q}+ \mathrm{{i}} \theta . \finish{aligned}$$
(12)
The flow maps to a semi-infinite strip in the \(\varOmega \)-airplane,where the wall BD is given past \(\theta =\pi -\beta \), and the vertical walls AB and AC are mapped onto the horizontal line \(\theta =0\), equally shown in Fig. 5.

Flow configuration in the t-airplane

Catamenia configuration in the \(\varOmega \)-plane
I finds that the Schwarz–Christoffel mapping from the \(\varOmega \)-plane to the t-plane is given by
$$\begin{aligned} \varOmega (t) = -2 \left( \frac{\beta }{\pi } - 1 \right) \left[ \tanh ^{-1}\left( \sqrt{\frac{(d+1)t}{d(t+1)}} \correct) - \tanh ^{-ane}\left( \sqrt{\frac{d+ane}{d}} \right) \correct] . \end{aligned}$$
(xiii)
When \(\beta =\pi \), we notice that \(\varOmega =0\), and the menstruation is simply a compatible stream. One can then obtain streamlines by integrating the identity
$$\begin{aligned} x_\phi + \mathrm{{i}} y_\phi = \mathrm{e}^{\varOmega }, \cease{aligned}$$
(fourteen)
along lines of constant \(\psi \). We perform this integration numerically by fixing \(\psi ={\bar{\psi }}\) and discretising \(\phi \). Nosotros note that nosotros truncate \(\phi \) sufficiently far upstream, say \(\phi \in [-\phi _A,\phi _D]\), where \(\phi _A\) is large enough such that the menstruation is approximately a uniform stream there. Hence, 1 tin can write \(z(-\phi _A+\mathrm{{i}} {\bar{\psi }}) = \mathrm{{i}}{\bar{\psi }}\), then we use the trapezoidal rule to integrate Eq. (14). Care must be taken when integrating at B (and later in the paper at C when \(\mu \ne \pi \)) due to the stagnation point singularity. For case, from Eq. (ix) we know that at B
$$\brainstorm{aligned} x_\phi \sim \left( \phi _B-\phi \right) ^{\beta /\pi -1}. \end{aligned}$$
(15)
We remove the singularity from the integral by writing
$$\begin{aligned} x(\phi )|_{\psi =0} = \int _{-\phi _A}^\phi \left[ x_\phi (\alpha )|_{\psi =0} - C_1 \left( \phi _B- \blastoff \right) ^{\beta /\pi -1} \right] \, \mathrm {d} \alpha + \int _{-\phi _A}^\phi C_1 \left( \phi _B- \alpha \correct) ^{\beta /\pi -1} \, \mathrm {d} \alpha . \end{aligned}$$
(16)
The concluding integral can be evaluated analytically, while nosotros evaluate the offset ane numerically using the trapezoidal rule. The constant \(C_1\) in this case can be found exactly using Eq. (13). Later in the paper, the value is approximated past matching the solution at the meshpoint closest to the singularity.
In the following section, we hash out a boundary integral method that tin be used to solve the model with gravity and surface tension.
Boundary integral method
In this section, we will present the start numerical scheme used to solve the model formulated in Sect. ii. The method allows u.s. to compute solutions including the furnishings of gravity and surface tension. We first express \(\11 \) in the form
$$\begin{aligned} u-\mathrm{{i}}five = \mathrm{e}^{\tau -\mathrm{{i}}\theta }. \stop{aligned}$$
(17)
We seek \(\tau (f)\) and \(\theta (f)\) as existent valued functions of the circuitous variable \(f=\phi +\mathrm{{i}}\psi \). Equally done in Sect. three, we again map the flow to the lower half t-aeroplane by writing the complex potential in the form of Eq. (ten). The method involves using Cauchy's integral formula to express the unknowns in terms of boundary values. Writing \(t=\gamma +\mathrm{{i}}\delta \), nosotros relate values of \(\tau \) in the f-plane with values in the t-plane past writing
$$\begin{aligned} \tau (f) = {\hat{\tau }}\left( \mathrm{e}^{-\pi f}\right) = {\lid{\tau }}\left( t \right) \terminate{aligned}$$
(eighteen)
with a similar equation for \({\hat{\theta }}\). The purlieus weather condition (iv-6) can then be written in the form
$$\brainstorm{aligned} {\hat{\theta }}(t)&= 0 \qquad \qquad \text {for} \,\,\, \gamma \in (-\infty ,-1), \,\,\, \delta =0, \stop{aligned}$$
(nineteen)
$$\begin{aligned} {\hat{\theta }}(t)&= \pi -\beta \,\,\quad \text {for} \,\,\, \gamma \in (0,d), \,\,\, \delta =0, \end{aligned}$$
(20)
$$\brainstorm{aligned} {\chapeau{\theta }}(t)&= 0 \qquad \qquad \text {for} \,\,\, \gamma \in (d,\infty ), \,\,\, \delta =0. \end{aligned}$$
(21)
Applying Cauchy's integral formula to the part \({\chapeau{\tau }}-\mathrm{{i}}{\hat{\theta }}\) in the t-plane, where we take a contour consisting of the real centrality and a semi-circumvolve of arbitrarily large radius in the lower half t-aeroplane, one can show that
$$\begin{aligned} {\hat{\tau }}(\gamma _0) - i{\chapeau{\theta }}(\gamma _0) = -\frac{one}{i \pi } \int _{-\infty }^{\infty } \frac{{\hat{\tau }}(\gamma ) - i{\hat{\theta }}(\gamma ) }{\gamma -\gamma _0} \, \mathrm {d} \gamma , \finish{aligned}$$
(22)
where \(\gamma _0\) is a point on the existent centrality in the t-aeroplane, and the integrals are evaluated in the Cauchy principle value sense. The real component of the above equation gives
$$\begin{aligned} {\hat{\tau }}(\gamma _0) = \frac{1}{\pi } \int _{-\infty }^{\infty } \frac{{\hat{\theta }}(\gamma )}{\gamma -\gamma _0} \, \mathrm {d} \gamma . \cease{aligned}$$
(23)
The boundary conditions (19–21) reduce Eq. (23) to
$$\begin{aligned} {\hat{\tau }}(\gamma _0) = \frac{one}{\pi } \int _{-1}^{0} \frac{{\chapeau{\theta }}(\gamma ) }{\gamma -\gamma _0} \, \mathrm {d} \gamma + \left( 1-\frac{\beta }{\pi }\right) \log \frac{|d - \gamma _0 |}{|\gamma _0 |}. \end{aligned}$$
(24)
The right-hand side of the to a higher place integral equation concerns simply values of \({\hat{\theta }}\) on the free surface (\(\gamma \in [-1,0]\)). Hence, setting \(\gamma _0\in [-1,0]\), we tin detect values of \({\chapeau{\tau }}\) on the free surface if we know values of \({\hat{\theta }}\). We note that the integral has a removable singularity at \(\gamma =\gamma _0\). We instead write
$$\begin{aligned} \frac{1}{\pi } \int _{-1}^{0} \frac{{\chapeau{\theta }}(\gamma )}{\gamma -\gamma _0} \, \mathrm {d} \gamma = \frac{one}{\pi } \int _{-ane}^{0} \frac{{\hat{\theta }}(\gamma ) - {\hat{\theta }}(\gamma _0)}{\gamma -\gamma _0} \, \mathrm {d} \gamma + \frac{{\hat{\theta }}(\gamma _0)}{\pi } \log \frac{|\gamma _0 |}{|one+\gamma _0 |}. \end{aligned}$$
(25)
We perform a change of variables on the integral, such that information technology is expressed in terms of \(\phi \). This results in
$$\begin{aligned} \tau (\phi _0+i)&= \frac{ane}{\pi } \int _{0}^{\infty } \frac{\theta (\phi +i) - \theta (\phi _0+i) }{\mathrm{e}^{-\pi (\phi _0-\phi )} - 1} \, \mathrm {d} \phi + \frac{\theta (\phi _0+i)}{\pi } \log \frac{|\gamma _0 |}{|ane+\gamma _0 |} +\, \left( 1-\frac{\beta }{\pi }\correct) \log \frac{|d - \gamma _0 |}{|\gamma _0 |}, \end{aligned}$$
(26)
where \(\gamma _0=-\mathrm{eastward}^{-\pi \phi _0}\). Bernoulli's equation (two) now reads
$$\begin{aligned} \mathrm{eastward}^{2\tau } - \frac{2}{F^2} x - \frac{2}{\alpha } \mathrm{eastward}^{\tau } \frac{\partial \theta }{\partial \phi } = B \end{aligned}$$
(27)
Information technology suffices to observe \(\theta (\phi )\) and \(\tau (\phi )\) that satisfy (26) and (27), which is done numerically, every bit described beneath.
Nosotros truncate the domain \(\phi \in [0,\infty ]\) to \(\phi \in [0,\phi _D]\), where \(\phi _D\) must exist called to be sufficiently large such that the solution becomes invariant to further increase in \(\phi _D\). We discretise \(\phi \) into N equally spaced points, given past
$$\begin{aligned} \phi _I= (I-i)h,\quad I=1,two\ldots ,Northward. \end{aligned}$$
(28)
We annotation \(h=\phi _D/(N-1)\). We have \(N-one\) midpoints \(\phi _I^Chiliad\), where
$$\brainstorm{aligned} \phi _I^M = \frac{\phi _I + \phi _{I+1}}{2}. \end{aligned}$$
(29)
We accept as unknown N values of \(\theta (\phi _I+i)\), which we shall announce \(\theta _I\). Ane can then find values of \(\theta (\phi _I^M+i)\), denoted \(\theta _I^M\), via fourth-order interpolation formulae. We note that the separation angle \(\mu \) is related to \(\theta \):
$$\begin{aligned} \theta _1 = \pi -\mu . \cease{aligned}$$
(30)
One tin find \(\tau \) at the midpoints \(\phi _I^M\) by evaluating Eq. (26) at \(\phi _I^M\). The integral is evaluated numerically using the trapezoidal rule. We satisfy Bernoulli'south equation at the midpoints \(\phi _I^M\), resulting in \(Northward-1\) equations. When \(\beta \ne \pi \), nosotros also fix West, the height of the pipe (nosotros describe before long how the value of Westward is recovered). Thus far, satisfying the boundary integral equation (26) and Bernoulli's equation ensure \(\tau \) and \(\theta \) are analytic, and satisfy the boundary conditions. The final equations required to close the arrangement depend on the type of solution sought. For example, if seeking a pure gravity solution with \(\beta =\pi /2\), then we have \(N+2\) unknowns: \(\theta _1\), \(\ldots \), \(\theta _N\), \(\phi _B\), and B. Given we already have North equations, the 2 equations which close the system are fixing \(\mu \), and setting \(\theta _N=\theta _{North-1}\) (such that the far-field is flat). If we seek gravity–capillary solutions with \(\beta =\pi /2\) (these solutions accept waves in the far-field), it is constitute that more quantities have to be stock-still to obtain a unique solution. In this example, the \(N+1\) unknowns are \(\theta _I\) and B. The boosted equation is given by fixing \(\mu \). A more detailed discussion on what must exist fixed and be allowed to vary for each instance is given in Sect. 6.
In the to a higher place, nosotros need values of x and \(\partial \theta /\partial \phi \) on the interface to satisfy Bernoulli's equation. Furthermore, we demand to evaluate Westward. Values of \(\partial \theta /\partial \phi \) are plant using four-betoken finite difference formulae on the discretised solution \(\theta _I\). Values of x and W are found every bit described below. The values of \(x_I = x(\phi _I+i)\) are evaluated by integrating the identity
$$\begin{aligned} x_\phi + \mathrm{{i}} y_\phi = \mathrm{e}^{-\tau +\mathrm{{i}}\theta }. \end{aligned}$$
(31)
Nosotros observe that
$$\brainstorm{aligned} x_I = \int _0^{\phi _I} \mathrm{e}^{-\tau } \cos (\theta (\phi +i)) \, \mathrm {d} \phi . \end{aligned}$$
(32)
This integral is evaluated numerically using the midpoint rule, ensuring to remove the singularity at C from the integral. Recall that locally, the flow behaves like
$$\begin{aligned} x_\phi + \mathrm{{i}} y_\phi = C_2 \phi ^{\mu /\pi -1}. \end{aligned}$$
(33)
This gives
$$\begin{aligned} x_{I+ane} = x_I + h \left( \mathrm{due east}^{-\tau _I^K} \sin (\theta _I^Thousand) - C_2 \left( \phi _I^M\right) ^{\mu /\pi -1} \right) + C_2 \frac{\pi }{\mu }\left( \phi _{I+1}^{\mu /\pi } - \phi _{I}^{\mu /\pi }\right) \finish{aligned}$$
(34)
where the constant \(C_2\) is approximated past equating the local behaviour (33) to the numerical solution (31) at the first midpoint \(\phi _1^One thousand\).
The elevation of the pipe W is found in the same style as discussed in Sect. 3. We numerically integrate Eq. (31) forth the streamlines \(\psi =0\) and \(\psi =1\). We again truncate \(\phi \rightarrow -\infty \) to \(\phi =-\phi _A\), ensuring \(\phi _A\) is sufficiently large that farther increment in \(\phi _A\) results in negligible modify in the value of West. We and so discretise \(\phi \in [-\phi _A,\phi _B]\) for \(\psi =0\) into \(Yard+1\) equally spaced points \(\phi _I\) via
$$\begin{aligned} \phi _I = -\phi _A + thou(I-1), \quad I=1,\ldots ,Thousand+1, \end{aligned}$$
(35)
and \(\phi \in [-\phi _A,0]\) for \(\psi =ane\) into \(L+1\) every bit spaced points \(\phi _I\) via
$$\begin{aligned} \phi _I = -\phi _A + l(I-1), \quad I=one,\ldots ,L+one, \terminate{aligned}$$
(36)
where \(k=(\phi _A+\phi _B)/M\) and \(l=\phi _A/50\). Nosotros know the values of \(\theta \) on the boundaries \(\psi =0\) and \(\psi =1\). The values of \(\tau (f)\) tin be found on AB (\(\psi =0\), \(\phi <\phi _B\)) via the identity
$$\begin{aligned} \tau (\phi _0) = -\frac{i}{\pi } \int _{0}^{\infty } \frac{\theta (\phi +i) }{\mathrm{east}^{-\pi (\phi _0-\phi )} + 1} \, \mathrm {d} \phi + \left( one-\frac{\beta }{\pi }\right) \log \frac{|d - \gamma _0 |}{|\gamma _0 |}. \end{aligned}$$
(37)
Meanwhile, the values of \(\tau \) tin can be plant on Ac (\(\psi =ane\), \(\phi <0\)) via the identity
$$\begin{aligned} \tau (\phi _0+i)&= \frac{1}{\pi } \int _{0}^{\infty } \frac{\theta (\phi +i) - \theta (i) }{\mathrm{east}^{-\pi (\phi _0-\phi )} - 1} \, \mathrm {d} \phi + \frac{\theta (i)}{\pi } \log \frac{|\gamma _0 |}{|i+\gamma _0 |} + \left( 1-\frac{\beta }{\pi }\right) \log \frac{|d - \gamma _0 |}{|\gamma _0 |}. \end{aligned}$$
(38)
The to a higher place integral is written such that the singularity that occurs as \(\phi _0\rightarrow 0\) is removed. The value Due west is then given by
$$\begin{aligned} W = \int _{-\phi _A}^{\phi _B} x_\phi |_{\psi =0} \, \mathrm {d} \phi - \int _{-\phi _A}^{0} x_\phi |_{\psi =1} \, \mathrm {d} \phi . \end{aligned}$$
(39)
The above integrals are computed numerically via the midpoint rule, where the singularities at B and C are again removed. When computing solutions, nosotros must ensure that the number of unknowns matches the number of equations. The number of parameters we require to gear up to obtain a unique solution depends on the parameter values considered, as discussed in Sect. 6. This concludes the description of the boundary integral method. In the post-obit section, we discuss the series truncation method.
Serial truncation method
In this section, nosotros will nowadays a second numerical scheme based on series truncation to compute fully nonlinear solutions to the organisation of equations (four)–(7). As with the method from the previous department, information technology also allows for the inclusion of gravity and surface tension. Withal, i weakness is that information technology can but compute solutions which far downstream approach a uniform stream. Hence, this method cannot compute solutions with gravity and surface tension when \(\beta =\pi /two\), since such solutions are found to arroyo a periodic wavetrain downstream. For a review of serial truncation methods practical to steady potential menses, see \(\S \)3 of [35]. This section volition follow closely the piece of work of [6, 7], who solved this problem for \(\beta =\pi \) with surface tension and gravity, and [eleven], who likewise devised a method to find solutions with gravity for \(\beta =\pi /ii\).

Flow configuration in the f-plane. Dashed curves are streamlines
The method one time once more involves conformally mapping the period domain to an auxiliary plane. This time we choose the southward-plane to be a unit semi-circumvolve (in the upper half-aeroplane). Given that the menses domain in the f-airplane is given by an infinite strip \(0\le \psi \le 1\), the mapping from f to s is found to exist
$$\begin{aligned} f(s) = \frac{i}{\pi } \log \left( \frac{4s}{(1-southward)^2} \right) . \terminate{aligned}$$
(40)
The f-plane and s-aeroplane are shown in Figs. 6 and seven, respectively. The bespeak A maps to \(s=0\), C to \(s=-i\), D to \(s=ane\), and B to \(s=s_B\), where
$$\begin{aligned} s_B = ane + 2\mathrm{due east}^{-\pi \phi _B} - ii\sqrt{\mathrm{eastward}^{-two\pi \phi _B} + \mathrm{e}^{-\pi \phi _B}}. \terminate{aligned}$$
(41)
The reflected portion of the flow, that is \(-one\le \psi \le 0\), is mapped to the semi-circle in the lower half-plane obtained when reflecting the image in Fig. 7 across the real axis. To ensure that the serial representation of \(\xi \) converges, we must remove all singularities of \(\xi \) in \(\{southward: |south |\le 1, \mathfrak {I}(s)\ge 0 \}\). The first singularity we will consider comes from the separation indicate C. The flow here behaves like the flow in a corner of angle \(\mu \). Using Eqs. (9) and (twoscore), one finds the singular behaviour
$$\brainstorm{aligned} \xi \sim (due south+1)^{two-2\mu /\pi },\quad \text {every bit} \,\,\, s\rightarrow -1. \finish{aligned}$$
(42)
Next, we consider the singularity at the tip of the wedge B. Similar to Eq. (42), the leading lodge atypical behaviour is that of flow in a corner of interior bending \(\beta \). Over again, using Eqs. (ix) and (40), one finds

Menstruum configuration in the s-plane. Dashed curves are streamlines
$$\begin{aligned} \xi \sim (s-s_B)^{1-\beta /\pi }\quad \text {every bit} \,\,\, s\rightarrow s_B. \end{aligned}$$
(43)
The final singularity is associated with the catamenia in the far-field D. The singularity has 2 possible behaviours. Kickoff, when \(\beta \in (\pi /two,\pi )\), it was shown by Birkhoff and Carter [i] that
$$\begin{aligned} \xi \sim z^{one/two} \sim f^{1/three}. \end{aligned}$$
(44)
Using Eq. (40), nosotros observe
$$\brainstorm{aligned} \xi \sim \left( - \log (i-s) \correct) ^{1/3} \quad \text {as} \,\,\, due south\rightarrow i. \end{aligned}$$
(45)
If \(\beta =\pi /2\), the far-field tin approach either a uniform stream or a periodic train of waves. Assume for now that the period approaches a uniform stream with velocity \(U_f\). The method in this section requires \(\xi \) to be divers at \(s=ane\), and hence tin can merely solve for solutions with flat far-fields. The downstream Froude number \(F_f\) and Weber number \(\alpha _f\) relate to F and \(\alpha \) via the equations
$$\brainstorm{aligned} F_f = U_f^{3/two} F \quad \blastoff _f = U_f \alpha . \end{aligned}$$
(46)
It is found that
$$\begin{aligned} \xi \sim i U_f + A \mathrm{e}^{-U_F \pi \lambda \phi }, \quad \text {as} \,\,\, \phi \rightarrow \infty , \end{aligned}$$
(47)
where \(\lambda \) is a root of the equation
$$\begin{aligned} \pi \lambda F_f^ii - \tan \left( \pi \lambda \correct) \left( ane - B_f \pi ^2 \lambda ^2 ) \correct) = 0. \end{aligned}$$
(48)
Hither, \(B_f\) is the downstream Bond number, given by \(B_f = F_f^2 /\alpha _f\). The in a higher place behaviour is found past linearising the flow most a compatible stream with speed \(U_f\). It is the dispersion relation for gravity–capillary waves, with a wavelength of \(\mathrm{{i}}\lambda \) (and hence a wavenumber \(k=2\pi \mathrm{{i}}/\lambda \)). Notation that the far-field has oscillations unless \(\lambda \) is real (see Eq. (47)). Equations (ten) and (47) imply that
$$\begin{aligned} \11 \sim \exp \left( A(1-south)^{2\lambda } \right) \quad \text {as} \,\,\, south\rightarrow 1. \end{aligned}$$
(49)
Therefore, nosotros advise 2 different representations for \(\xi \). In the starting time case, when \(\beta \ne \pi /2\), we write
$$\brainstorm{aligned} \xi = \frac{\left( - \log C (1-s) \right) ^{i/three}}{\left( - \log C \correct) ^{1/three}} \left( \frac{s_B-s}{s_B}\right) ^{1-\beta /\pi } (s+one)^{2-two\mu /\pi } \exp \left( \sum _{due north=one}^\infty a_n south^due north\right) , \finish{aligned}$$
(l)
where C is a fixed constant satisfying \(0<C<0.five\), such that \(\xi \) is purely real on the line \(s\in [-one,s_B]\). It can exist seen that (fifty) satisfies the atypical behaviour (42), (43), and (45), and that \(\xi (0) = 1\). This series, with \(\beta =\pi \), was used in [7, eight, 36]. If \(\beta =\pi /ii\), then we instead take
$$\begin{aligned} \xi = \left( \frac{s_B-s}{s_B}\right) ^{1/2} (s+one)^{2-2\mu /\pi } \exp \left( -A+A(1-s)^{ii\lambda } + \sum _{n=ane}^\infty a_n due south^n\right) , \end{aligned}$$
(51)
where A and \(\lambda \) are unknown, and have to be found as part of the solution. We note here that with \(\beta =\pi /2\), no waveless solutions were institute when \(F_f\ne 0\) and \(B_f\ne 0\). Hence, the series (51) can only exist used to compute solutions with no surface tension. When \(B_f=0\), then from Eq. (48) we notice that \(\lambda \) is real for \(F_f>1\) (i.east. solutions are waveless when the flow in the far-field is super-critical). The constant \(\lambda \) is taken to be the smallest positive root of (48). Nosotros note that [11] used a like series representation for \(\xi \) when considering \(\beta =\pi /2\), except they did not include the term \(\exp (A(1-s)^{2\lambda })\) in their expansion. They instead used
$$\brainstorm{aligned} \eleven = \left( \frac{s_B-s}{s_B}\right) ^{one/2} (s+1)^{2-2\mu /\pi } \exp \left( \sum _{due north=1}^\infty a_n s^n\right) . \end{aligned}$$
(52)
We found that, truncating the series after a sufficient number of coefficients, their results agree inside graphical accuracy with those computed using the serial (51). Notwithstanding, the coefficients \(a_n\) disuse at a much slower rate without this new exponential term, as discussed in Sect. 6.3.
We truncate both series later on \(N-1\) terms. When \(\beta \ne \pi /2\), this results in \(N+1\) unknowns (\(a_1\), \(\ldots \), \(a_{N-1}\), \(\mu \), B). The free surface in the s-plane is given by \(south=\mathrm{due east}^{\mathrm{{i}}\sigma }\) with \(\sigma \in [0,\pi ]\). We discretise \(\sigma \) into \(N+1\) equally space points, given by
$$\begin{aligned} \sigma _I = \pi \frac{(I-1/two)\pi }{ Due north+1}, \quad I=1,\ldots ,N+1. \finish{aligned}$$
(53)
The series representation of \(\xi \) has been constructed such that the kinematic boundary conditions and the governing equation are satisfied. It is left to satisfy the dynamic boundary condition (7) at each meshpoint \(\sigma _I\), which is given by
$$\begin{aligned} (u^2 + v^2) - \frac{2}{F^two} x - \frac{two\pi }{\alpha } \left( u \frac{\fractional 5}{\partial \sigma } - v \frac{\partial u}{\partial \sigma }\right) (u^2+v^2)^{-1/2} \tan \frac{\sigma }{2}= B. \cease{aligned}$$
(54)
This gives usa \(N+one\) equations for \(N+1\) unknowns, which are solved via Newton's method. When \(\beta =\pi /2\), we have ii boosted unknowns, A and \(\lambda \). Therefore, nosotros satisfy Eq. (seven) at \(N+two\) every bit spaced points in \(\sigma \), given by
$$\begin{aligned} \sigma _I = \frac{(I-1/2)\pi }{ N+2}, \quad I=one,\ldots ,N+two. \end{aligned}$$
(55)
Nosotros also satisfy Eq. (48), where \(F_f\) is calculated using Eq. (46), and \(U_f\) can be found by evaluating (51) at \(s=ane\). Hence, we have obtained \(N+3\) equations for \(N+3\) unknowns, a organization which can be solved numerically using Newton's method.
The profile of the interface is obtained by numerically integrating the identity
$$\brainstorm{aligned} x_\sigma +\mathrm{{i}} y_\sigma = - \frac{one}{\pi } \cot \left( \frac{\sigma }{ii}\right) \frac{1}{\xi } \quad \text {for} \,\,\, s=\mathrm{e}^{\mathrm{{i}}\sigma }, \, \sigma \in [0,\pi ]. \end{aligned}$$
(56)
We do this using the trapezoidal rule on the discritised domain \(\sigma _I\). The peak of the pipage W is plant in the same mode as was discussed in Sect. 4. We numerically integrate equation
$$\brainstorm{aligned} x_\phi + \mathrm{{i}} y_\phi = \frac{1}{\xi }, \finish{aligned}$$
(57)
along the streamlines \(\psi =0\) and \(\psi =one\) from \(\phi =-\phi _A\) to \(\phi =\phi _B\) and \(\phi =0\), respectively. Values of \(\11 \) can exist plant for a given \(\phi \) and \(\psi \) by finding the the corresponding value of due south from Eq. (40), then using the relevant series solution for \(\11 \). The same discretisation and numerical integration as was washed in Sect. 4 is used to compute W.
This concludes the clarification of the series truncation method. In the post-obit section, nosotros discuss the results of the paper.
Results
Nosotros brainstorm by briefly recapping the results when \(\beta =\pi \), which are found in [6,vii,8], since the results here help inform us on what to look for the solution space for other values of \(\beta \).
Results for \(\beta =\pi \)
First, consider the case when \(\blastoff ^{-1}=0\). The flow configuration is as shown in Fig. 2a. The model corresponds to catamenia exiting a pipe with no obstruction, or plane bubbles rising at a constant velocity. For each value of F, at that place is a unique solution. Information technology is found that in that location exists a critical Froude number \(F_C\approx 0.51\), such that when \(F<F_C\) the separation angle \(\mu =\pi /2\), while if \(F>F_C\), and so \(\mu =\pi \), as illustrated in Table 1. The solutions with \(\mu =\pi /ii\) are referred to as smooth bubbles, while \(\mu =\pi \) solutions are cusped bubbles. There is also a unique pointed bubble with \(\mu =two\pi /3\) when \(F=F_C\). When surface tension is nonzero (that is \(\alpha ^{-ane}\ne 0\)), the angle \(\mu \) becomes continuously dependent on F. This is shown in Fig. viii for \(\blastoff =5\) and \(\alpha =20\). It can be seen that as F decreases, the value \(\mu \) oscillates about \(\mu =\pi /two\). Furthermore, every bit \(\alpha \) is increased, the amplitude and wavelength of the oscillations decrease. Allow us denote \(F_1(\blastoff )\) as the largest value of F where the curves intersect for a given \(\alpha \), \(F_2(\alpha )\) as the second largest such value, and so on. These branches \(F_i(\alpha )\) are branches of smooth bubbling, and are monotonically increasing with \(\alpha \). As \(\alpha \rightarrow \infty \), all of these branches converge onto a single value, \(F=F^*\). Information technology is establish that \(F^*\approx 0.318\). The mechanism by which a unique solution is called from a possible set of solutions, by including surface tension (or other forces), and taking said forces to zero, is known every bit solution selection. A similar phenomenon is seen in Saffman–Taylor fingering [37, 38]. The solutions on the primary branch \(F_1(\alpha )\) smoothen profiles with no oscillations. On the higher order branches of smooth bubbles, the profiles develop oscillations [39]. Information technology is of interest to note that the solution space of axisymmetric Taylor bubbles exhibit much of the same behaviour [39, twoscore].

Relationship betwixt \(\mu \) and F for \(\alpha =5\) (solid curve) and \(\alpha =20\) (dashed bend) for \(\beta =\pi \). The dotted lines are \(\mu =\pi /2\) and \(\mu =\pi \)
Results for \(\beta \in (\pi /2,\pi )\)
The flow configuration for \(\beta \in (\pi /2,\pi )\) is shown in Fig. 2b. The results are qualitatively similar to the results establish for \(\beta =\pi \). Offset, consider the case when \(\alpha ^{-ane}=0\). For a stock-still \(\beta \), we now have two costless parameters, F and \(\phi _B\). In the computations, instead of fixing \(\phi _B\) and recovering West a posteriori, we chose to gear up W and allow \(\phi _B\) to vary. Note that the parameter \(\phi _B\) is related to \(s_B\) in the series truncation method via Eq. (41), and d in the purlieus integral method via Eq. (11). Unsurprisingly, information technology is found that \(\phi _B\) monotonically increases as Westward is increased. When surface tension is ignored, we once more meet a critical value \(F_C\), where the solutions have the properties given in Table 1. Information technology is now the case that \(F_C\) has dependence on \(\beta \) and W. We conjecture that as \(Due west\rightarrow \infty \), \(F_C\) has a finite limiting value equivalent to the \(F_C\) found by Vanden-Broeck [8] for plane bubbles. This comes from the fact that as Due west increases, the pipe is moved farther away from the wedge, and the behaviour of the flow near the separation indicate becomes closer to that of flow exiting a piping without an obstruction (\(\beta =\pi \)). The dotted and dashed curves in Fig. 9 bear witness the dependence of \(F_c\) on W for \(\beta =two\pi /3\) and \(\beta =5\pi /6\), respectively. We experience difficulties with computing \(F=F_C\) solutions for values of W greater than that shown in the figure due to our inability to get enough meshpoints distributed along the free surface for these more extreme profiles.

Value of \(F_C\) for varying West. The solid curve is for \(\beta =\pi /2\), dashed curve \(\beta =2\pi /3\), and dotted curve \(\beta =5\pi /6\)
Streamlines to typical solutions are shown in Fig. 10 for \(\beta =ii\pi /3\) and \(W=1\). The bold lines in the effigy stand for to solid boundaries, the dashed curves interior streamline, and the solid curve the free surface. Effigy (a) has \(F<F_C\), (b) \(F=F_C\), and figure (c) \(F>F_C\). The crosses in Fig. 10c is the gratis streamline solution derived in Sect. 3. Since the solution in Fig. 10c is for \(F=20\), one would expect reasonable agreement with the gratis streamline solution (\(F\rightarrow \infty \)). It can be seen that the understanding is very practiced near the separation point. However, every bit i moves further forth the profile, the solutions offset to deviate, due to the unlike singular behaviour downstream (the free streamline solution approaches a compatible stream, every bit opposed to the behaviour (45)). This is shown in Fig. 10d, where we accept plotted the menstruum farther downstream for the \(F=xx\) solution. The solutions presented are computed using the serial truncation method described in Sect. five. However, we as well computed the solutions using the boundary integral method from Sect. 4, as shown by the circles in figure (a) and (b). As can be seen, the profiles almost overlap. The agreement betwixt the analytic solution and ii numerical schemes provides a convincing check on the methods used.

Solutions for \(\beta =2\pi /iii\), \(West=1\), \(\alpha ^{-1} = 0\), and a \(F=0.3\), b \(F=F_C(\beta ,W)\approx 0.464\), and c \(F=20\). The crosses in c is the corresponding \(F\rightarrow \infty \) solution. d shows the solution in c further downstream. Only half a solution (\(0\le \psi \le i\)) is shown. The bold curves are the boundaries, the solid curve and circles the free surface (computed using the serial truncation method and boundary integral method, respectively), and the dashed curves are streamlines
When surface tension is included, similar results to the plane chimera are found. Ane finds that the separation angle \(\mu \) has a continuous dependence on F. For a given \(\alpha \), the value of \(\mu \) oscillates about \(\pi /2\) for values of \(F<F_C\). Meanwhile, when \(F\rightarrow \infty \), \(\mu \rightarrow \pi \). This is the same behaviour as shown in Fig. eight for \(\beta =\pi \). One could once again use the solution selection procedure to notice a unique solution to the zero surface tension problem with a separation angle of \(\mu =\pi /2\). Notwithstanding, there is no clear concrete significance to the selected solution. Another similarity with the \(\beta =\pi \) solution space is that the solutions on the college mode branches also develop oscillations on the free surface, as shown in Fig. 11. Profiles of solutions with \(\beta =2\pi /3\), \(Due west=0.5\), and \(\alpha =5\) are shown. The values of F are called such that \(\mu =\pi /2\).

a Shows profiles of solutions with \(\beta =two\pi /three\), \(West=0.5\), \(\blastoff =5\), and \(\mu =\pi /ii\). The values of F are \(F=0.276\), 0.195, 0.150, 0.121 for the solid bend, dotted bend, dashed bend, and dotted-dashed curve, respectively. The bolder lines are the solid boundaries. b shows a blow upwards of the region near the separation point
Results for \(\beta =\pi /2\)
Finally, we shall discuss the solution space when \(\beta =\pi /ii\). This problem was already solved numerically using a serial truncation method when surface tension is ignored [11]. However, as mentioned previously in Sect. v, the authors failed to remove an additional singularity caused past the far-field decay of the gratuitous surface (see Eq. (47)). The results presented in the paper agree with our calculations within graphical accuracy. However, the disuse of the coefficients of the truncated series \(a_n\) is weaker, as shown in Table 2. The table shows the society of the coefficients for the solutions with \(\phi _B=1.5\) for two values of F. It can be seen this boosted singularity is of import to remove for convergence of the series representation of \(\eleven \).
It was found by [eleven] that, every bit with values of \(\beta \) in the range \(\beta \in (\pi /two,\pi ]\), fixing F and West results in a unique solution. In this case, the far-field is not an minute jet but instead a uniform stream. There once again exists a critical value \(F_C\), dependent on W, such that the separation angle \(\mu \) agrees with the behaviour seen in Table ane. The relation between \(F_C\) and W is shown by the solid curve in Fig. 9.
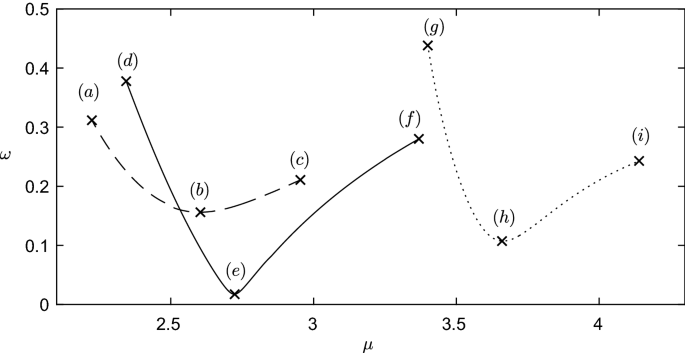
Some solution branches for gravity–capillary free surface flows with \(\beta =\pi /2\). All solution branches take \(\alpha =2.5\). The branch a–c has parameter values \(F=0.75\), \(W=1.six\), and \(\phi _B=one.1\). The branch d–f has \(F=1\), \(W=i.6\), and \(\phi _B=ane.ane\). The branch grand–i has \(F=1\), \(W=1\), and \(\phi _B=0.1175\). In the computations, nosotros vary \(\mu \) and plot the branch confronting \(\omega \). The profiles at the points a–i are shown in Fig. xiii
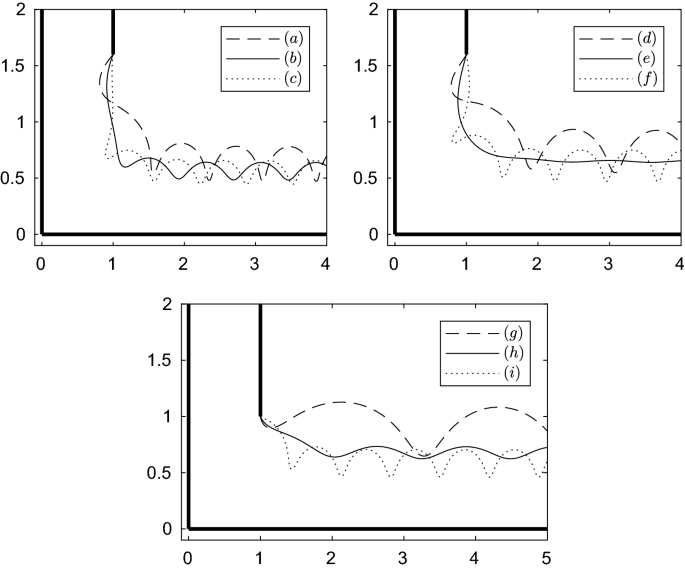
The profiles respective to the points a–i in Fig. 12
The solution space when surface tension is included is more complicated than when \(\beta \in (\pi /2,\pi ]\). Nosotros discover that fixing F and \(\alpha \) is not sufficient to produce a unique solution. We observe we must also fix two additional parameters, which we cull to be \(\mu \) and \(\phi _B\). Solutions with waves in the far-field are witnessed. We denote the amplitude of the waves in the far-field as \(\omega \). We compute some solution branches, fixing F, \(\alpha \), \(\phi _B\), and Due west, and and then assuasive \(\mu \) to vary. Having fixed the parameters as described in a higher place, it is found that solutions do not exist for all values of \(\mu \). Instead, solutions exist within a range of values of \(\mu \), the range depending on the stock-still parameters. Once one solution has been found, 1 tin notice the complete solution branch via continuation in \(\mu \). The solution branches starting time and end on solutions with larger \(\omega \). For all parameters tested, starting from the smallest value of \(\mu \) for which there is a solution, \(\omega \) monotonically decreases to a minimum, and then monotonically increases to the largest possible value of \(\mu \). This tin can be seen in Fig. 12, where we testify some typical solution branches for various values parameter values. The branches are plotted in (\(\mu \),\(\omega \)) space. Some typical profiles are shown in Fig. 13. It was found for the parameters tested that the branch never touched the \(\omega \) axis. Hence, no waveless gravity–capillary profiles were found.

Profile of the solution labelled (d) in Fig. 12 computed for diverse values of \(\phi _D\) and h. The solid curve is for \(\phi _D=12\) and \(h=0.01\), the dashed curve for \(\phi _D=24\) and \(h=0.01\), and the crosses for \(\phi _D=12\) and \(h=0.005\) (not all the meshpoints are plotted with crosses). The solutions develop inaccuracies in the far-field caused by truncation of the space integrals, which are rectified by further extending the domain
To check the convergence of the solutions with waves in the far-field, nosotros vary both the mesh spacing h and domain truncation \(\phi _D\). It tin be seen in Fig. 14 that the understanding upon mesh refinement is good. We besides observe that the last wavelength on the figure is spurious: this is expected, due to the truncation of the computational domain. Farther extending \(\phi _D\) results in a profile that agrees almost exactly upwards to the last wavelength of the shorter solution. This ensures that domain truncation does non cause errors to the flow shut to the separation betoken, and that our numerical approximation of a finite length far-field is valid, equally long equally we compute enough wavelengths downward from the pipe.
Conclusion
In conclusion, nosotros have provided an extensive numerical study of the model shown in Fig. 1. We have considered 3 case. First, when surface tension and gravity are negligible, we derived an verbal free streamline solution. Next, when gravity is included but surface tension is neglected, we recovered previously found results for \(\beta =\pi \) and \(\beta =\pi /2\), equally well as finding results for \(\beta \in (\pi /2,\pi )\). Finally, when surface tension is also included, nosotros recomputed the results for \(\beta =\pi \), while the results for \(\beta \in [\pi /2,\pi )\) are novel. The case when \(\beta =\pi /2\) has a richer solution space, since the far-field condition allows for waves to occur on the free surface. Good agreement between the ii numerical methods employed, as well every bit the exact free streamline solution, provides a check on the accurateness of the numerical results presented.
References
-
Birkhoff G, Carter D (1957) Rising plane bubbles. J. Math. Mech. 6:769–779
-
Chandler TGJ, Trinh PH (2018) Complex singularities near the intersection of a costless surface and wall. Role one. Vertical jets and ascent bubbles. J. Fluid Mech. 856:323–350
-
Garabedian PR (1957) On steady-state bubbling generated by Taylor instability. Proc. R. Soc. Lond. A 241:423–431
-
Garabedian PR (1985) A remark well-nigh pointed bubbling. Commun. Pure App. Math. 38:609–612
-
Modi V (1985) Comment on "Bubbles rising in a tube and jets falling from a nozzle". Phys. Fluids 28:3432–3433
-
Vanden-Broeck JM (1984a) Bubbles rising in a tube and jets falling from a nozzle. Phys. Fluids 27:1090–1093
-
Vanden-Broeck JM (1984b) Ascension bubbles in a ii-dimensional tube with surface tension. Phys. Fluids 27:2604–2607
-
Vanden-Broeck JM (1986) Pointed bubbling rising in a two-dimensional tube. Phys. Fluids 29:1343–1344
-
Couet B, Strumolo GS, Dukler AE (1986) Modeling two-dimensional big bubbles in a rectangular aqueduct of finite width. Phy. Fluids 29:2367–2372
-
Kessler DA, Levine H (1989) Velocity selection for Taylor bubbles. Phy. Rev. A 39:5462–5465
-
Christodoulides P, Dias F (2010) Impact of a falling jet. J. Fluid Mech. 657:22–35
-
Forbes LK, Schwartz LW (1982) Free-surface catamenia over a semicircular obstacle. J. Fluid Mech. 114:299–314
-
Rex AC, Bloor MIG (1987) Free-surface period over a footstep. J. Fluid Mech. 182:193–208
-
Wiryanto LH, Widjaja J, Supriyanto HB (2011) Free-surface flow under a sluice gate from deep h2o. Math. Sci. Soc. Bull. Malays. 34:601–609
-
Tooley Southward, Vanden-Broeck JM (2002) Waves and singularities in nonlinear capillary free-surface flows. J. Eng. Math. 43:89–99
-
Folder BJ, Vanden-Broeck JM (2005) Gratis surface flows by surfboards and sluice gates. Eur. J. App. Math. 16:601–619
-
Hunter JK, Vanden-Broeck JM (1983) Solitary and periodic gravity-capillary waves of finite amplitude. J. Fluid Mech. 134:205–219
-
Schwartz L, Vanden-Broeck JM (1979) Numerical solution of the verbal equations for capillary-gravity waves. J. Fluid Mech. 95:119–139
-
Vanden-Broeck JM (1983a) Some new gravity waves in water of finite depth. Phys. Fluids 26:2385–2387
-
Părău E, Vanden-Broeck JM (2002) Nonlinear two-and 3-dimensional gratuitous surface flows due to moving disturbances. Eur. J. Mech. Fluids B 21:643–656
-
Love AEH (1891) On the theory of discontinuous fluid motions in ii dimensions. Cambridge Philosophical Lodge, Cambridge
-
Hopkinson B (1897) On discontinuous fluid motions involving sources and vortices. Proc. Lond. Math. Due south. one:142–164
-
Doak A, Vanden-Broeck JM (2020) New exotic capillary free-surface flows. J. Fluid Mech. Rapids 899:R4
-
Birkhoff G, Zarantonello E (1957) Jets, wakes, and cavities, vol two. Elsevier, Amsterdam
-
Dagan Chiliad, Tulin MP (1972) Ii-dimensional gratis-surface gravity flow by blunt bodies. J. Fluid Mech. 51:529–543
-
Ackerberg RC (1975) The effects of capillarity on costless-streamline separation. J. Fluid Mech. lxx:333–352
-
Cumberbatch E, Norbury J (1979) Capillary modification of the singularity at a free-streamline separation betoken. Q. J. Mech. Appl. Math. 32:303–312
-
Vanden-Broeck JM (1981) The influence of capillarity on cavitating flow past a flat plate. Q. J. Mech. Appl. Math. 34:465–473
-
Vanden-Broeck JM (1983b) The influence of surface tension on cavitating flow past a curved obstacle. J. Fluid Mech. 133:255–264
-
Vanden-Broeck JM (2004) Nonlinear capillary free-surface flows. J. Eng. Math. 50:415–426
-
Eggers J, Smith AF (2010) Free streamline flows with singularities. J. Fluid Mech. 647:187–200
-
Ackerberg RC, Liu TJ (1987) The effects of capillarity on the wrinkle coefficient of a jet emanating from a slot. Phys. Fluids 30:289–296
-
Gasmi A, Mekias H (2003) The upshot of surface tension on the contraction coefficient of a jet. J. Phys. A: Math. Gen. 36:851–862
-
Vanden-Broeck JM (1984c) The effect of surface tension on the shape of the Kirchhoff jet. Phys. Fluids 27:1933–1936
-
Vanden-Broeck JM (2010) Gravity-capillary free-surface flows. Cambridge University Press, Cambridge
-
Daripa P (2000) The fastest polish Taylor chimera. Appl. Num. Math. 34:373–379
-
McLean JW, Saffman PG (1981) The effect of surface tension on the shape of fingers in a Hele Shaw jail cell. J. Fluid Mech. 102:455–469
-
Vanden-Broeck JM (1983c) Fingers in a Hele-Shaw cell with surface tension. Phys. Fluids 26:2033–2034
-
Doak A, Vanden-Broeck JM (2018) Solution selection of axisymmetric Taylor bubbles. J. Fluid Mech. 843:518–535
-
Levine H, Yang Y (1990) A ascent bubble in a tube. Phys. Fluids A two:542–546
Author information
Affiliations
Respective author
Boosted information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Jean-Marc Vanden-Broeck was supported in part by EPSRC under Grant EP/NO18559/ane.
Rights and permissions
Open Admission This article is licensed nether a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, every bit long equally yous give appropriate credit to the original author(southward) and the source, provide a link to the Creative Eatables licence, and indicate if changes were fabricated. The images or other third political party material in this article are included in the commodity's Artistic Eatables licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended apply is not permitted by statutory regulation or exceeds the permitted use, y'all will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/four.0/.
Reprints and Permissions
Near this article
Cite this article
Doak, A., Vanden-Broeck, JM. Nonlinear 2-dimensional free surface solutions of flow exiting a pipage and impacting a wedge. J Eng Math 126, eight (2021). https://doi.org/ten.1007/s10665-020-10086-z
-
Received:
-
Accustomed:
-
Published:
-
DOI : https://doi.org/10.1007/s10665-020-10086-z
Keywords
- Free surface flows
- Gravity–capillary flows
- Numerical methods
albaradociary1948.blogspot.com
Source: https://link.springer.com/article/10.1007/s10665-020-10086-z
0 Response to "Consider the Two Dimensional Agains the Flat Plate"
Post a Comment